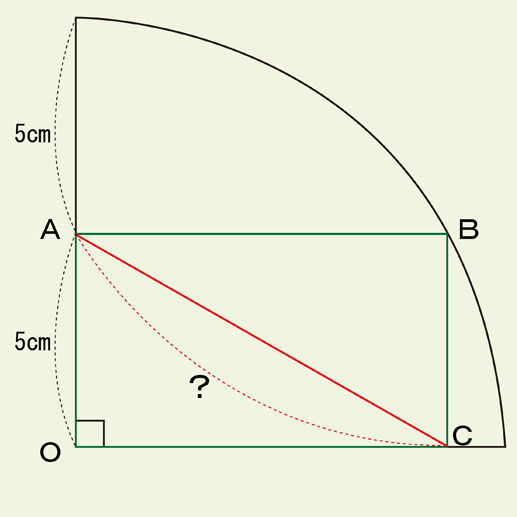
図形問題には面積を求めたり角の大きさを求めるものなど多種多様の問題が考えられます。どの種類の問題にしても解き方がたくさんあり楽しいものです。今回は線分の長さを求めるという問題です。中心角の大きさが90°であるおうぎ形の中に長方形OABCを置きました。頂点AとCはおうぎ形の半径上にあり、頂点Bは円周上にあります。線分ACの長さを求めて下さい。
- 問題
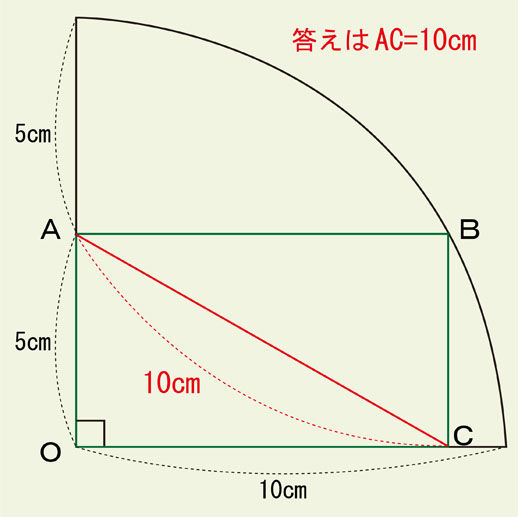
線分ACの長さを求めて下さい。
このままではお手上げ状態です。
長さが示されている線分以外で、長さのわかる線分はないでしょうか。

長方形の性質を覚えていますか。「向かいあっている辺の長さは等しい」です。ということは、AO=BCということですから、BC=5cmということがわかります。
では、ABとOCの長さは何cmでしょうか。この長さがわかれば、昔、習ったことのある「三平方の定理」を使ってACの長さを求められますね。
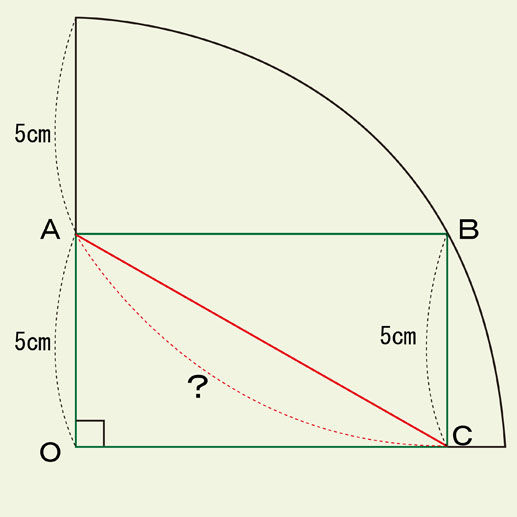
「三平方の定理」? なんだか難しそうです。別の方法はないでしょうか。もっと簡単にACの長さを求められないものでしょうか。
見方を変えてみましょう。この円の半径は何cmでしょうか。
図からわかるように、この円の半径は10cmです。5cm+5cm=10cmということからわかります。オレンジ色の線分も半径です。半径はこれ以外にも無数に引くことができます。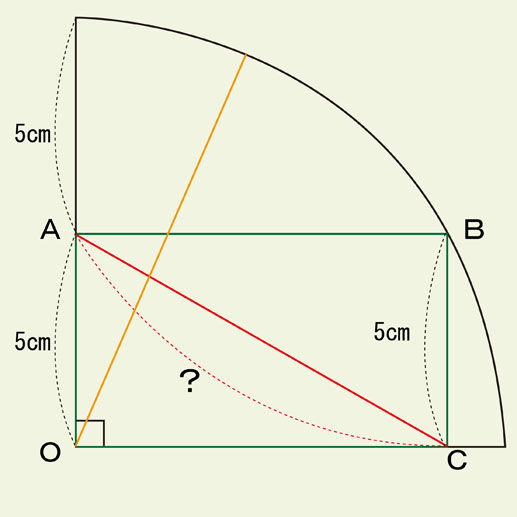
線分OBも半径です。
線分OBは、長方形OABCの対角線でもあります。長方形には対角線が2本あり、その長さは等しいとわかっていますから、OB=10cmです。そして、もう1本の対角線は・・・、線分ACです。
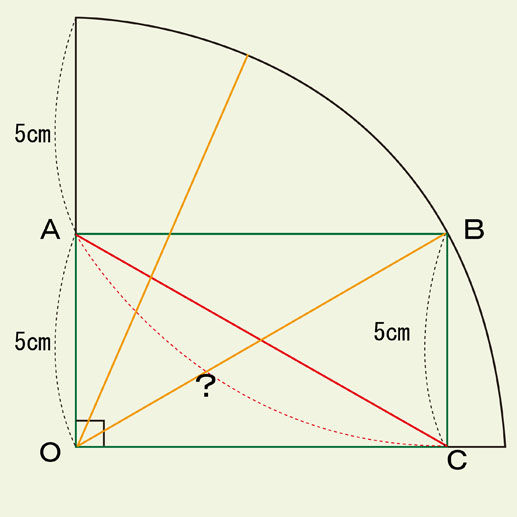
-答えです
OB=AC、かつ、OB=10cmです。つまり、AC=10cmです。
この問題を見たときに、AC=OBで、OBが半径だということに気付けば、AC=10cmという答えはすぐに出てきました。しかし、人間の目というものは不思議なもので、ACが半径と等しい長さだとしてもその描かれ方によってはなかなか見抜きにくいものです。
このようなちょっとひっかけのような問題も、数多く解いていくうちにすぐに見抜けるようになります。
次回の図形問題ではひっかけるような問題ではないものを出したいと考えています。


一瞬で解ったぞ!
算数も数学も苦手だけどw
点Oが円の中心って前提が無いと、この証明成り立たなくない?
点Oが円の中心なんて前提いらなくない?
そもそも円じゃなくて扇型と定義してるワケだし、頭固すぎー